Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Эти три точки называют вершинами треугольника, а отрезки — сторонами треугольника.
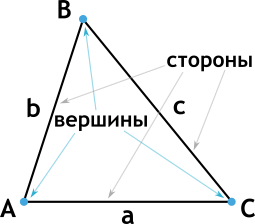
На рисунке мы видим три вершины, которые обозначены буквами A, B и C.
Также на рисунке изображены 3 стороны треугольника. Их можно обозначать по вершинам, которые их ограничивают. Например, сторона AB, сторона BC и сторона AC. Но для удобства вершины можно обозначать короче. В примере на рисунке сторону AB можно обозначить как b, BC как c, а AC как a.
Формула для вычисления площади треугольника по 3 сторонам
Для нахождения площади треугольника по трем сторонам используют формулу Герона.
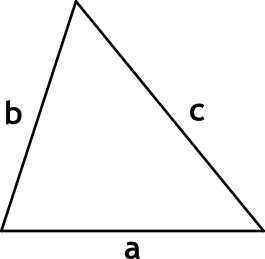
a, b, c - длины сторон треугольника,
p - полупериметр треугольника.
Примеры решения задач по нахождению площади треугольника
Задача 1
Решение
Перед тем, как искать площадь треугольника по трем сторонам, необходимо найти его полупериметр. Для этого сложим длины его сторон и разделим сумму на 2:
p = \dfrac{a+b+c}{2} = \dfrac{6+6+8}{2} = \dfrac{20}{2} = 10Теперь, зная полупериметр, можем воспользоваться формулой Герона и найти площадь треугольника:
S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{10(10-6)(10-6)(10-8)}=\sqrt{10 \cdot 4 \cdot 4 \cdot 2} = \sqrt{320} \approx 17.88854Ответ: \sqrt{320} \approx 17.88854
Осталось проверить ответ с помощью калькулятора .
Задача 2
Решение
Как и в задаче выше начнем решение с нахождения полупериметра треугольника:
p = \dfrac{a+b+c}{2} = \dfrac{5+7+6}{2} = \dfrac{18}{2} = 9Далее подставим значения в формулой площади треугольника и найти ее:
S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{9(9-5)(9-7)(9-6)}=\sqrt{9 \cdot 4 \cdot 2 \cdot 3} = \sqrt{216} \approx 14.69694Ответ: \sqrt{216} \approx 14.69694
Осталось проверить ответ с помощью калькулятора .
Формула Герона применяется в различных областях, где необходимо находить площадь треугольника, в том числе:
- В геометрии для вычисления площади треугольников, например, при решении задач на нахождение площади или при вычислении высоты треугольника.
- В архитектуре и строительстве для расчета площади треугольных конструкций, например, крыш, заборов, деревянных конструкций и т.д.
- В физике для определения площади поверхности треугольных объектов, например, площади основания при вычислении объема пирамиды.
- В тригонометрии для решения задач, связанных с треугольниками.
- В механике для вычисления площади треугольной области, ограниченной маятником при расчете периода колебаний.
В целом, формула Герона широко используется в различных областях, где требуется находить площадь треугольника через три стороны, и является одной из наиболее распространенных формул геометрии.