Площадь треугольника через основание и высоту
{S = \dfrac{1}{2} \cdot a \cdot h}
Найти площадь
Известные данные
Сторона a
Высота h
Результат в
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать

Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника - равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.

  1. Калькулятор площади треугольника
  2. Площадь треугольника
    1. через основание и высоту
    2. через две стороны и угол между ними
    3. через сторону и два прилежащих угла
    4. через радиус описанной окружности и 3 стороны
    5. через радиус вписанной окружности и 3 стороны
    6. по формуле Герона
  3. Площадь прямоугольного треугольника
    1. через катеты
    2. через гипотенузу и прилежащий угол
    3. через катет и прилежащий угол
    4. через радиус вписанной окружности и гипотенузу
    5. через вписанную окружность
    6. по формуле Герона
    7. через катет и гипотенузу
  4. Площадь равнобедренного треугольника
    1. через основание и сторону
    2. через основание, боковую сторону и угол
    3. через основание и высоту
    4. через боковые стороны и угол между ними
    5. через основание и угол между боковыми сторонами
  5. Площадь равностороннего треугольника
    1. через сторону
    2. через высоту
    3. через радиус описанной окружности
    4. через радиус вписанной окружности
  6. Примеры задач

Площадь треугольника

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

Площадь треугольника через основание и высоту

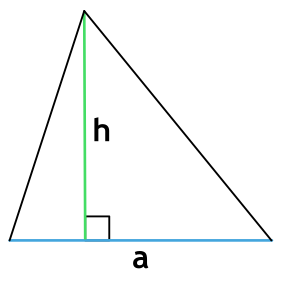
Площадь треугольника через основание и высоту
{S = \dfrac{1}{2} \cdot a \cdot h}

a - длина основания

h - высота, проведенная к основанию

Площадь треугольника через две стороны и угол между ними

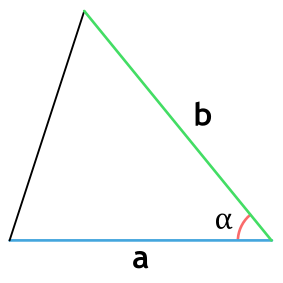
Площадь треугольника через две стороны и угол между ними
{S = \dfrac{1}{2} \cdot a \cdot b \cdot \sin(\alpha)}

a и b - стороны треугольника

α - угол между сторонами a и b

Площадь треугольника через сторону и два прилежащих угла

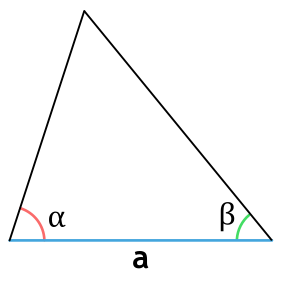
Площадь треугольника через сторону и два прилежащих угла
{S = \dfrac{a^2}{2} \cdot \dfrac{\sin{(\alpha)} \cdot \sin{(\beta)}}{sin{(\gamma)}}} {\gamma = 180 - (\alpha + \beta)}

a - сторона треугольника

α и β - прилежащие к стороне a углы

Площадь треугольника через радиус описанной окружности и 3 стороны

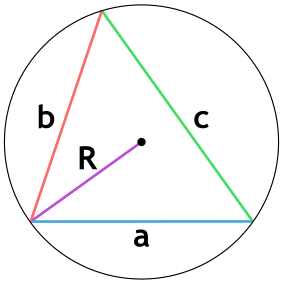
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = \dfrac{a \cdot b \cdot c}{4 \cdot R}}

a, b и c - стороны треугольника

R - радиус описанной окружности

Площадь треугольника через радиус вписанной окружности и 3 стороны

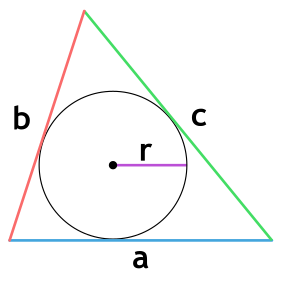
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r \cdot \dfrac{a + b + c}{2}}

a, b и c - стороны треугольника

r - радиус вписанной окружности

Площадь треугольника по формуле Герона

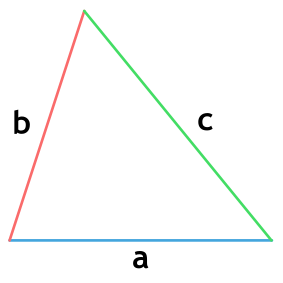
Площадь треугольника по формуле Герона
{S = \sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)}} {p= \dfrac{a+b+c}{2}}

a, b и c - стороны треугольника

p - полупериметр треугольника

Площадь прямоугольного треугольника

Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).

Площадь прямоугольного треугольника через катеты

Площадь прямоугольного треугольника через катеты
{S = \dfrac{1}{2} \cdot a \cdot b}

a и b - стороны треугольника

Площадь прямоугольного треугольника через гипотенузу и прилежащий угол

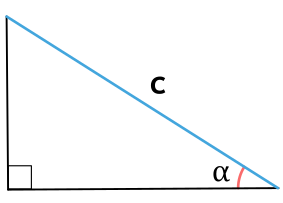
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = \dfrac{1}{4} \cdot c^2 \cdot \sin{(2 \alpha)}}

c - гипотенуза прямоугольного треугольника

α - прилежащий к гипотенузе c угол

Площадь прямоугольного треугольника через катет и прилежащий угол

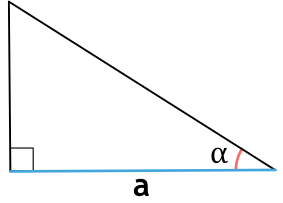
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = \dfrac{1}{2} \cdot a^2 \cdot \tg{(\alpha)}}

a - катет прямоугольного треугольника

α - прилежащий к катету a угол

Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу

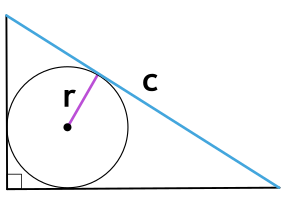
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r \cdot (r+c)}

r - радиус вписанной окружности

c - гипотенуза прямоугольного треугольника

Площадь прямоугольного треугольника через вписанную окружность

Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 \cdot c_2}

с1 и с2 - отрезки, полученные делением гипотенузы точкой касания окружности

Площадь прямоугольного треугольника по формуле Герона

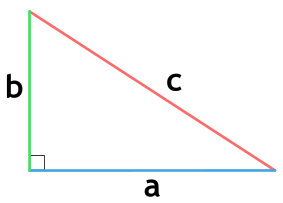
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) \cdot (p-b)} {p= \dfrac{a+b+c}{2}}

a, b и c - стороны треугольника

p - полупериметр треугольника

Площадь прямоугольного треугольника через катет и гипотенузу

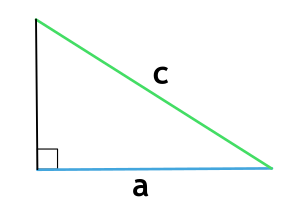
Площадь прямоугольного треугольника через катет и гипотенузу
{S = \dfrac{1}{2} \cdot a \cdot \sqrt{c^2 - a^2}}

a - катет прямоугольного треугольника

c - гипотенуза прямоугольного треугольника

Площадь равнобедренного треугольника

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.

Площадь равнобедренного треугольника через основание и сторону

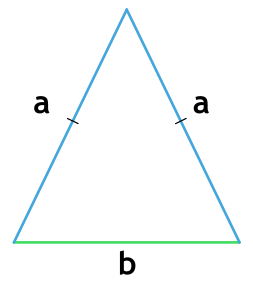
Площадь равнобедренного треугольника через основание и сторону
{S = \dfrac{b}{4} \sqrt{4a^2 - b^2}}

a - боковая сторона равнобедренного треугольника

b - основание равнобедренного треугольника

Площадь равнобедренного треугольника через основание, сторону и угол

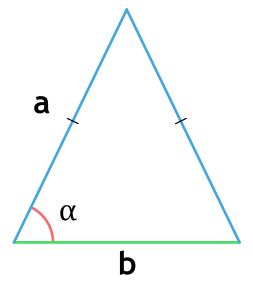
Площадь равнобедренного треугольника через основание, сторону и угол
{S = \dfrac{1}{2} \cdot a \cdot b \cdot \sin{(\alpha)}}

a - боковая сторона равнобедренного треугольника

b - основание равнобедренного треугольника

α - угол между основанием и боковой стороной

Площадь равнобедренного треугольника через основание и высоту

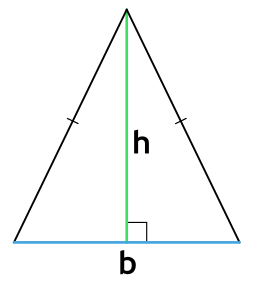
Площадь равнобедренного треугольника через основание и высоту
{S = \dfrac{1}{2} \cdot b \cdot h}

b - основание равнобедренного треугольника

h - высота, проведенная к основанию равнобедренного треугольника

Площадь равнобедренного треугольника через боковые стороны и угол между ними

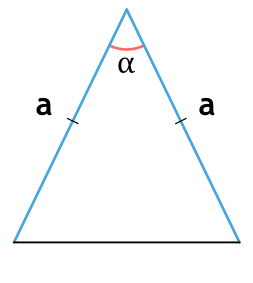
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = \dfrac{1}{2} \cdot a^2 \cdot \sin(\alpha)}

a - боковые стороны равнобедренного треугольника

α - угол между боковыми сторонами

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = \dfrac{b^2}{4 \cdot \tg {( \dfrac{\alpha}{2} )}}}

b - основание равнобедренного треугольника

α - угол между боковыми сторонами

Площадь равностороннего треугольника

Равносторонний треугольник - треугольник, у которого все стороны равны.

Площадь равностороннего треугольника через сторону

Площадь равностороннего треугольника через сторону
{S = \dfrac{\sqrt{3} \cdot a^2}{4}}

a - сторона равностороннего треугольника

Площадь равностороннего треугольника через высоту

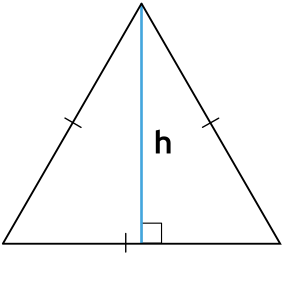
Площадь равностороннего треугольника через высоту
{S = \dfrac{h^2}{\sqrt{3}}}

h - высота равностороннего треугольника

Площадь равностороннего треугольника через радиус описанной окружности

Площадь равностороннего треугольника через радиус описанной окружности
{S = \dfrac{3 \sqrt{3} \cdot R^2}{4}}

R - радиус описанной окружности

Площадь равностороннего треугольника через радиус вписанной окружности

Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 \sqrt{3} \cdot r^2}

r - радиус описанной окружности

Примеры задач на нахождение площади треугольника

Задача 1

Найдите площадь треугольника со сторонами 13 14 15.

Решение

Для решения задачи воспользуемся формулой Герона.

S = \sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)}

Для начала нам необходимо найти полупериметр p:

p= \dfrac{a+b+c}{2}p= \dfrac{13+14+15}{2}= \dfrac{42}{2} = 21

Теперь можем подставить его в формулу Герона и найти ответ:

S = \sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)} = \sqrt{21 \cdot (21-13) \cdot (21-14) \cdot (21-15)} = \sqrt{21 \cdot (8) \cdot (7) \cdot (6)} = \sqrt{21 \cdot 336} = \sqrt{7056} = 84 \: см^2

Ответ: 84 см²

Убедимся в правильности решения с помощью калькулятора .

Задача 2

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.

Решение

Воспользуемся формулой.

S = \dfrac{1}{2} \cdot a \cdot \sqrt{c^2 - a^2} = \dfrac{1}{2} \cdot 28 \cdot \sqrt{100^2 - 28^2} = \dfrac{1}{2} \cdot 28 \cdot \sqrt{10000 - 784} = \dfrac{1}{2} \cdot 28 \cdot \sqrt{9216} = \dfrac{1}{2} \cdot 28 \cdot 96 = 14 \cdot 96 = 1344 \: см^2

Ответ: 1344 см²

Проверим ответ на калькуляторе .

Задача 3

Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.

Решение

Задача аналогична предыдущей, поэтому решение очень похоже.

S = \dfrac{1}{2} \cdot a \cdot \sqrt{c^2 - a^2} = \dfrac{1}{2} \cdot 15 \cdot \sqrt{17^2 - 15^2} = \dfrac{1}{2} \cdot 15 \cdot \sqrt{289 - 225} = \dfrac{1}{2} \cdot 15 \cdot \sqrt{64} = \dfrac{1}{2} \cdot 15 \cdot 8 = 15 \cdot 4 = 60 \: см^2

Ответ: 60 см²

Проверка .

Задача 4

Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.

Решение

Для решения задачи воспользуемся формулой.

S = \dfrac{1}{4} \cdot c^2 \cdot \sin{(2 \alpha)} = \dfrac{1}{4} \cdot 40^2 \cdot \sin{(2 \cdot 60°)} = \dfrac{1}{4} \cdot 1600 \cdot \sin{(120°)} = 400 \cdot \dfrac{\sqrt{3}}{2} = 200 \sqrt{3} \: см^2 \approx 346.41016 \: см^2

Ответ: 200 \sqrt{3} \: см^2 \approx 346.41016 \: см^2

Проверка .

Задача 5

Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.

Решение

В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.

S = \dfrac{b}{4} \sqrt{4a^2 - b^2} = \dfrac{4}{4} \sqrt{4 \cdot 7^2 - 4^2} = \sqrt{4 \cdot 49 - 16} = \sqrt{196 - 16} = \sqrt{180} = \sqrt{36 \cdot 5} = 6\sqrt{5} \: см^2 \approx 13.41641 \: см^2

Ответ: 6\sqrt{5} \: см^2 \approx 13.41641

Проверка .

Задача 6

Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.

Решение

Решим эту задачу по анологии с предыдущей.

S = \dfrac{b}{4} \sqrt{4a^2 - b^2} = \dfrac{30}{4} \sqrt{4 \cdot 17^2 - 30^2} = \dfrac{30}{4} \sqrt{4 \cdot 289 - 900} = \dfrac{30}{4} \sqrt{1156 - 900} = \dfrac{30}{4} \sqrt{256} = \dfrac{30}{4} \cdot 16= 30 \cdot 4 = 120 \: см^2

Ответ: 120 см²

Проверка .

Задача 7

Найдите площадь равностороннего треугольника со стороной 12 см.

Решение

Используем для решения задачи формулу.

S = \dfrac{\sqrt{3} \cdot a^2}{4} = \dfrac{\sqrt{3} \cdot 12^2}{4} = \dfrac{\sqrt{3} \cdot 144}{4} = 36 \sqrt{3} \: см^2 \approx 62.35383 \: см^2

Ответ: 36 \sqrt{3} \: см^2 \approx 62.35383 \: см^2

Проверка .