Площадь параллелограмма через сторону и высоту
{S = a \cdot h}
Найти площадь параллелограмма
Сторона a
Высота h
Результат в
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать

На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные - основание, высоту, стороны, диагонали и углы между ними и получите ответ.

Параллелограмм - это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).

Содержание:
  1. калькулятор площади параллелограмма
  2. формула площади параллелограмма через сторону и высоту
  3. формула площади параллелограмма через две стороны и угол между ними
  4. формула площади параллелограмма через диагонали и угол между ними
  5. примеры задач

Формула площади параллелограмма через сторону и высоту

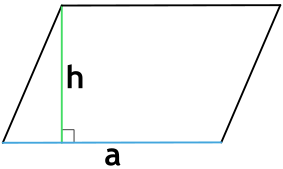
Площадь параллелограмма через сторону и высоту
{S = a \cdot h}

a - сторона параллелограмма

h - высота параллелограмма

Формула площади параллелограмма через две стороны и угол между ними

Площадь параллелограмма через две стороны и угол между ними
{S=a \cdot b \cdot \sin(\alpha)}

a, b - стороны параллелограмма

α - угол между сторонами a и b

Формула площади параллелограмма через диагонали и угол между ними

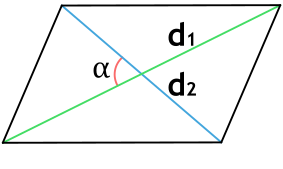
Площадь параллелограмма через диагонали и угол между ними
{S = \dfrac{1}{2} \cdot d_1 \cdot d_2 \cdot \sin(\alpha)}

d1, d2 - диагонали параллелограмма

α - угол между диагоналями

Примеры задач на нахождение площади параллелограмма

Задача 1

Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.

Решение

Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.

S = a \cdot b \cdot \sin(\alpha) = 9 \cdot 12 \cdot \sin(60) = 108 \cdot \sin(60) = 108 \cdot 0.866 \approx 93.53074 \: см^2

Ответ: 108 \cdot 0.866 \approx 93.53074 \: см^2

Мы можем проверить ответ с помощью калькулятора .

Задача 2

Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.

Решение

Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.

S = a \cdot b \cdot \sin(\alpha) = 8 \cdot 12 \cdot \sin(30) = 96 \cdot \sin(30) = 96 \cdot 0.5 = 48 \: см^2

Ответ: 48 см²

И снова проверить ответ нам поможет калькулятор .

Задача 3

Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.

Решение

В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.

S = a \cdot h = 12 \cdot 8 = 96 \: см^2

Ответ: 96 см²

И снова проверить ответ нам поможет калькулятор .