На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Формула объема шара через радиус

R - радиус шара
Формула объема шара через диаметр
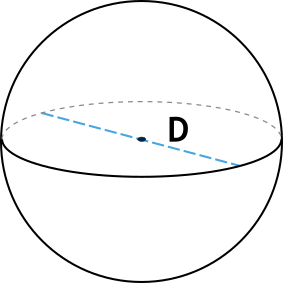
D - диаметр шара
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2\pi r}
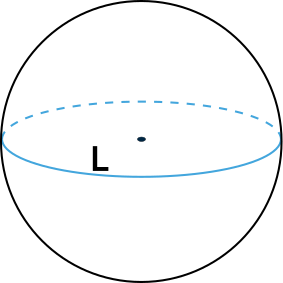
L - длина окружности
Формула объема шара через площадь поверхности
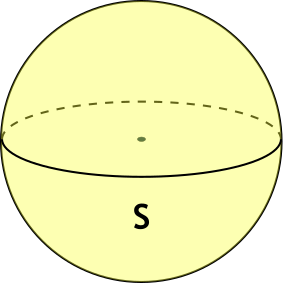
S - площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = \dfrac{4}{3} \pi R^3 = \dfrac{4}{3} \pi \cdot 12^3 = \dfrac{4}{3} \pi \cdot 1728 = \dfrac{4 \cdot 1728}{3} \pi = 2304 \cdot \pi \: см^3 \approx 7238.22947 \: см^3Ответ: 2304 \cdot \pi \: см^3 \approx 7238.22947 \: см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = \dfrac{1}{6} \pi D^3 = \dfrac{1}{6} \pi \cdot 12^3 = \dfrac{1}{6} \pi \cdot 1728 = \dfrac{1728}{6} \pi = 288 \pi \: см^3 \approx 904.77868 \: см^3Ответ: 288 \pi \: см^3 \approx 904.77868 \: см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Решение
Эта задача аналогична задаче 2.
V = \dfrac{1}{6} \pi D^3 = \dfrac{1}{6} \pi \cdot 6^3 = \dfrac{1}{6} \pi \cdot 216 = \dfrac{216}{6} \pi = 36 \pi \: см^3 \approx 113.09734 \: см^3Ответ: 36 \pi \: см^3 \approx 113.09734 \: см^3
И снова в проверке ответа нам поможет калькулятор .