Усеченный конус - фигура, которую можно получить из конуса, если через него провести сечение, параллельное основанию.
Справедливо и другое определение.
Усеченный конус - тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.
Калькулятор объема конуса и формулы для расчета находится здесь.
Чтобы найти объем усеченного конуса необходимо знать три его характеристики - высоту (h), радиус нижнего основания (R1) и радиус верхнего основания (R2). Кроме того существует вторая формула объема усеченного конуса, для которой необходимо знать высоту конуса, а также площади его верхнего и нижнего оснований.
Формула объема усеченного конуса через радиусы оснований и высоту
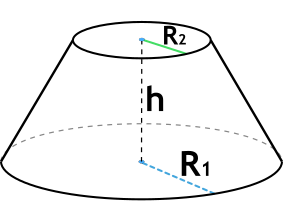
h - высота усеченного конуса
R1 - радиус нижнего основания
R2 - радиус верхнего основания
Формула объема усеченного конуса через площади оснований и высоту
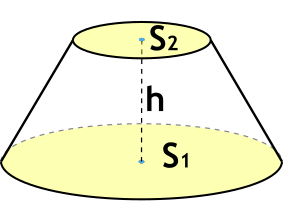
h - высота усеченного конуса
S1 - площадь нижнего основания
S2 - площадь верхнего основания
Примеры задач на нахождение объема усеченного конуса
Задача 1
Решение
Для решения используем формулу объема усеченного конуса через высоту и радиусы оснований. Подставим известные нам значения в формулу и произведем расчет.
V=\dfrac {1}{3} \pi h (R_1^2 + R_1 \cdot R_2 + R_2^2) = \dfrac {1}{3} \pi \cdot 3 \cdot (2^2 + 2 \cdot 1 + 1^2) = \dfrac {1}{3} \pi \cdot 3 \cdot (4 + 2 + 1) = \dfrac {1}{3} \pi \cdot 3 \cdot 7 = \dfrac {1}{3} \pi \cdot 21 = \dfrac {21}{3} \pi = 7 \pi \: см^3 \approx 21.99115 \: см^3Ответ: 7 \pi \: см^3 \approx 21.99115 \: см^3
Полученный ответ легко проверить с помощью калькулятора .