Площадь трапеции через основания и высоту
{S = \dfrac{1}{2} (a + b) \cdot h}
Найти площадь
Известные данные
Сторона a
Сторона b
Высота h
Результат в
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать

Привет, друзья! Сегодня мы поговорим о такой интересной геометрической фигуре, как трапеция. А конкретнее - разберемся, как найти ее площадь. Многие считают эту тему сложной, но на самом деле все не так страшно. Давайте разбираться вместе!

Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций - обычная, равнобедренная (равнобокая).

  1. Калькулятор площади трапеции
  2. Что такое трапеция?
  3. Элементы трапеции
  4. Виды трапеций
  5. Свойства трапеции
  6. Отличие трапеции от других четырёхугольников
  7. Площадь трапеции
    1. через основания и высоту
    2. через среднюю линию и высоту
    3. через диагонали и среднюю линию
    4. через 4 стороны
    5. через диагонали и угол между ними
    6. через основания и углы при основании
    7. через площади треугольников
    8. через диагонали и высоту
    9. через радиус вписанной окружности и основания
    10. через перпендикулярные диагонали
  8. Площадь равнобедренной (равнобокой) трапеции
    1. через основания и высоту
    2. через 3 стороны (формула Брахмагупты)
    3. через верхнее основание, боковую сторону и угол при нижнем основании
    4. через нижнее основание, боковую сторону и угол при нижнем основании
    5. через основания и угол
    6. через диагонали и угол между ними
    7. через боковую сторону, угол при основании и среднюю линию
    8. через радиус вписанной окружности и угол при основании
  9. Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
    1. через высоту (диаметр вписанной окружности) и угол при основании
    2. через основания и угол при основании
    3. через основания и радиус вписанной окружности
    4. через основания
    5. через основания и боковую сторону
    6. через основания и среднюю линию
  10. Примеры задач

Что такое трапеция?

Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие — нет. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами.

Трапеция

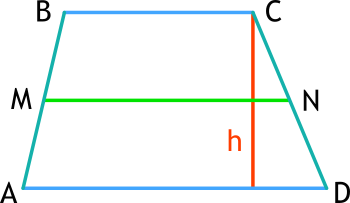
Элементы трапеции

У трапеции есть несколько ключевых элементов, которые важно знать для вычисления её площади:

  • Основания — параллельные стороны трапеции (AD и BC).
  • Боковые стороны — непараллельные стороны (AB и СВ).
  • Высота — перпендикуляр, опущенный из любой точки одного основания на прямую, содержащую другое основание (h).
  • Средняя линия — отрезок, соединяющий середины боковых сторон (MN).

Высота трапеции играет ключевую роль при вычислении площади. Она всегда перпендикулярна основаниям.

Трапеция, средняя линия и высота трапеции
Трапеция, средняя линия и высота трапеции

Виды трапеций

В зависимости от особенностей боковых сторон и углов выделяют несколько видов трапеций:

Вид трапеции Особенности Пример применения
Равнобедренная Боковые стороны равны Крыши домов, навесы
Прямоугольная Один из углов при основании — прямой Откосы окон, пандусы
Произвольная Все стороны и углы разные Нестандартные архитектурные элементы

Каждый вид трапеции имеет свои особенности, но формула для вычисления площади одинакова для всех видов.

Свойства трапеции

Трапеция обладает интересными свойствами, которые помогают в расчётах:

  • Сумма углов в трапеции, как и в любом четырёхугольнике, равна 360°.
  • Средняя линия трапеции параллельна основаниям и равна их полусумме.
  • Диагонали трапеции делят её на четыре треугольника.

Особенно полезно свойство средней линии. Если мы обозначим среднюю линию как m, то:

{m = (a + b) / 2}

где a и b — длины оснований.

Это свойство даёт нам ещё один способ вычисления площади трапеции: умножение средней линии на высоту.

Отличие трапеции от других четырёхугольников

Новички часто путают трапецию с другими четырёхугольниками. В таблице ниже показаны главные отличия:

Четырёхугольник Главное отличие от трапеции
Параллелограмм Все противоположные стороны параллельны
Ромб Все стороны равны
Прямоугольник Все углы прямые
Квадрат Все стороны равны и все углы прямые

Интересно, что параллелограмм можно считать особым случаем трапеции, когда обе пары противоположных сторон параллельны.

Итак, трапеция — это четырёхугольник с двумя параллельными сторонами (основаниями). Именно параллельность оснований и расстояние между ними (высота) дают нам возможность легко вычислить площадь трапеции с помощью простой формулы, о которой мы поговорим в следующем абзаце.

Площадь трапеции через основания и высоту

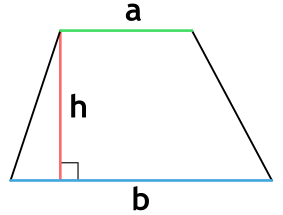
Площадь трапеции через основания и высоту
{S = \dfrac{1}{2} (a + b) \cdot h}

a и b - основания трапеции

h - высота, проведенная к основанию

Площадь трапеции через среднюю линию и высоту

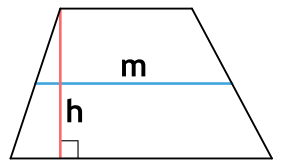
Площадь трапеции через среднюю линию и высоту
{S = m \cdot h}

m - средняя линия трапеции

h - высота трапеции

Площадь трапеции через диагонали и среднюю линию

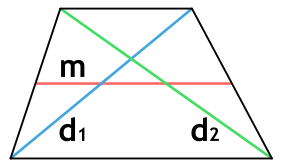
Площадь трапеции через диагонали и среднюю линию
{S = \sqrt{p(p-d_1)(p-d_2)(p-2m)}} {p = \dfrac{d_1+d_2+2m}{2}}

d1 и d2 - диагонали трапеции

m - средняя линия трапеции

Площадь трапеции через 4 стороны

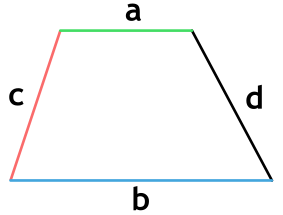
Площадь трапеции через 4 стороны
{S = \dfrac{a+b}{2} \sqrt{c^2 - {\Big( \dfrac{(a-b)^2 + c^2 - d^2}{2(a-b)} \Big)}^2}}

a, b, c и d - стороны трапеции

Площадь трапеции через диагонали и угол между ними

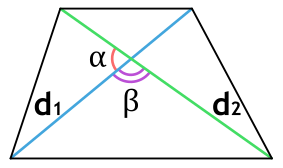
Площадь трапеции через диагонали и угол между ними
{S = \dfrac{d_1 \cdot d_2}{2}\cdot \sin(\alpha); S = \dfrac{d_1 \cdot d_2}{2}\cdot \sin(\beta)}

d1 и d2 - диагонали трапеции

α или β - угол между диагоналями трапеции

Площадь трапеции через основания и углы при основании

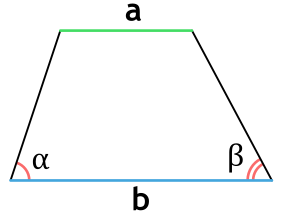
Площадь трапеции через основания и углы при основании
{S = \dfrac{b^2 - a^2}{2} \cdot \dfrac{\sin(\alpha) \cdot \sin(\beta)}{\sin(\alpha + \beta)}}

a и b - основания трапеции

α или β - прилежащие к основанию трапеции углы

Площадь трапеции через площади треугольников

Площадь трапеции через площади треугольников
{S = (\sqrt{S_1} + \sqrt{S_2})^2}

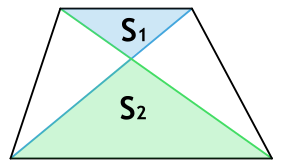
S1 и S2 - площади образованных пересечением диагоналей трапеции треугольников

Площадь трапеции через диагонали и высоту

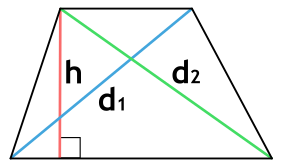
Площадь трапеции через диагонали и высоту
{S = \dfrac{\sqrt{{d_2}^2-h^2}+\sqrt{{d_1}^2-h^2}}{2} \cdot h}

d1 и d2 - диагонали трапеции

h - высота трапеции

Площадь трапеции через радиус вписанной окружности и основания

Площадь трапеции через радиус вписанной окружности и основания
{S = (a+b)\cdot r}

a и b - основания трапеции

r - радиус вписанной в трапецию окружности

Площадь трапеции через перпендикулярные диагонали

Площадь трапеции через перпендикулярные диагонали
{S = \dfrac{1}{2} \cdot d_1 \cdot d_2}

d1 и d2 - перпендикулярные диагонали трапеции

Площадь равнобедренной (равнобокой) трапеции

Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.

Площадь равнобедренной трапеции через основания и высоту

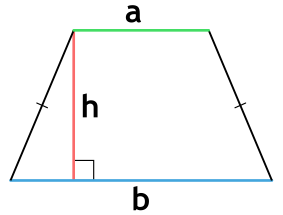
Площадь равнобедренной трапеции через основания и высоту
{S = \dfrac{a+b}{2} \cdot h}

a и b - основания равнобедренной трапеции

h - высота, проведенная к основанию равнобедренной трапеции

Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)
{S = \sqrt{(p-a)(p-b)(p-c)^2}} {p = \dfrac{a+b+2c}{2}}

a и b - основания равнобедренной трапеции

c - боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании
{S = c \cdot \sin(\alpha) \cdot (a+c \cdot \cos(\alpha))}

a - верхнее основание равнобедренной трапеции

c - боковая сторона равнобедренной трапеции

α - прилежащие к нижнему основанию трапеции углы

Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании

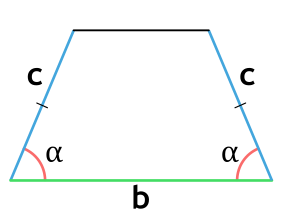
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
{S = c \cdot \sin(\alpha) \cdot (b-c \cdot \cos(\alpha))}

b - нижнее основание равнобедренной трапеции

c - боковая сторона равнобедренной трапеции

α - прилежащий к нижнему основанию трапеции угол

Площадь равнобедренной трапеции через основания и угол

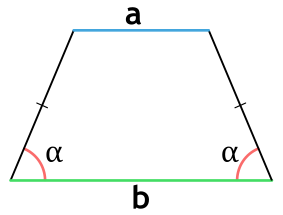
Площадь равнобедренной трапеции через основания и угол
{S = \dfrac{(b^2-a^2) \cdot \tg(\alpha)}{4}}

a и b - основания равнобедренной трапеции

α - прилежащий к основанию трапеции угол

Площадь равнобедренной трапеции через диагонали и угол между ними

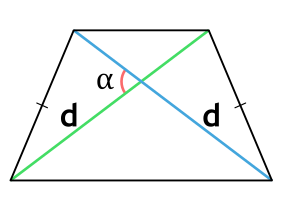
Площадь равнобедренной трапеции через диагонали и угол между ними
{S = \dfrac{1}{2}d^2 \cdot \sin(\alpha)}

a - диагональ равнобедренной трапеции

α - угол между диагоналями равнобедренной трапеции

Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию

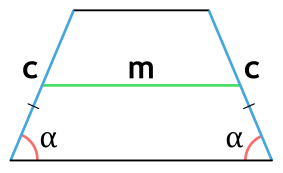
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
{S = m \cdot c \cdot \sin(\alpha)}

m - средняя линия равнобедренной трапеции

c - боковая сторона равнобедренной трапеции

α - угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании
{S = \dfrac{4r^2}{\sin(\alpha)}}

r - радиус вписанной окружности

α - угол при основании равнобедренной трапеции

Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность

В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании
{S = \dfrac{h^2}{\sin(\alpha)}}

h - высота равнобедренной трапеции

α - угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании

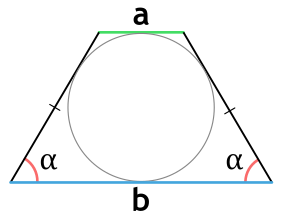
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
{S = \dfrac{a \cdot b}{\sin(\alpha)}}

a и b - основания равнобедренной трапеции

α - угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности

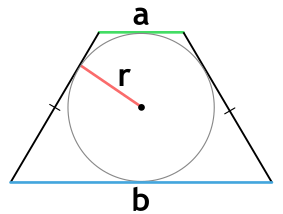
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
{S = r(a+b); r=\dfrac{\sqrt{a \cdot b}}{2}}

a и b - основания равнобедренной трапеции

r - радиус вписанной окружности

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания
{S = \sqrt{a \cdot b} \cdot \dfrac{a+b}{2}}

a и b - основания равнобедренной трапеции

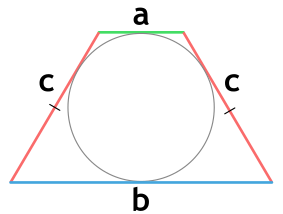
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
{S = c \cdot \sqrt{a \cdot b}}

a и b - основания равнобедренной трапеции

c - боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию

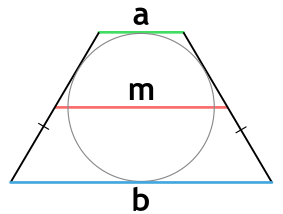
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
{S = m \cdot \sqrt{a \cdot b}}

a и b - основания равнобедренной трапеции

m - средняя линия равнобедренной трапеции

Примеры задач на нахождение площади трапеции

Задача 1

Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.

Решение

Для решения задачи воспользуемся первой формулой.

S = \dfrac{1}{2} (a + b) \cdot h = \dfrac{1}{2} (6 + 9) \cdot 5 = \dfrac{1}{2} \cdot 15 \cdot 5 = \dfrac{1}{2} \cdot 75 = 37\dfrac{1}{2} \: см^2

Ответ: 37.5 см²

Полученный ответ легко проверить с помощью калькулятора .

Задача 2

Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.

Решение

С решением этой задачи нам поможет вторая формула.

S = m \cdot h = 18 \cdot 9 = 162 \: см^2

Ответ: 162 см²

Воспользуемся калькулятором для проверки результата.

Задача 3

Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.

Решение

Для решения этой задачи нам поможет третья формула.

На первом этапе вычислим p:

p = \dfrac{d_1+d_2+2m}{2} = \dfrac{10+8+2 \cdot 3}{2} = \dfrac{10+8+6}{2} = \dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = \sqrt{p(p-d_1)(p-d_2)(p-2m)} = \sqrt{12(12-10)(12-8)(12-2 \cdot 3)} = \sqrt{12 \cdot 2 \cdot 4 \cdot 6} = \sqrt{576} = 24 \: см^2

Ответ: 24 см²

Осталось проверить полученный ответ.

Задача 4

Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.

Решение

Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.

На первом этапе вычислим p:

p = \dfrac{d_1+d_2+2m}{2} = \dfrac{17+15+ 2 \cdot 4}{2} = \dfrac{17+15+8}{2} = \dfrac{40}{2} = 20

А теперь можно вычислить площадь трапеции:

S = \sqrt{p(p-d_1)(p-d_2)(p-2m)} = \sqrt{20(20-17)(20-15)(20-2 \cdot 4)} = \sqrt{20 \cdot 3 \cdot 5 \cdot 12} = \sqrt{3600} = 60 \: см^2

Ответ: 60 см²

Проверка .

Задача 5

Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.

Решение

Еще одна типовая задача. Повторим действия как в задачах выше.

На первом этапе вычислим p:

p = \dfrac{d_1+d_2+2m}{2} = \dfrac{8+6+ 2 \cdot 5}{2} = \dfrac{8+6+10}{2} = \dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = \sqrt{p(p-d_1)(p-d_2)(p-2m)} = \sqrt{12(12-8)(12-6)(12-2 \cdot 5)} = \sqrt{12 \cdot 4 \cdot 6 \cdot 2} = \sqrt{576} = 24 \: см^2

Ответ: 24 см²

Проверка .

Задача 6

Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.

Решение

Для решения этой задачи используем формулу Брахмагупты.

Сначала вычислим p:

p = \dfrac{a+b+2c}{2} = \dfrac{5+17+2 \cdot 10}{2} = \dfrac{22+20}{2} = \dfrac{42}{2} = 21

А теперь можно вычислить площадь трапеции:

S = \sqrt{(p-a)(p-b)(p-c)^2} = \sqrt{(21-5)(21-17)(21-10)^2} = \sqrt{16 \cdot 4 \cdot 11^2} = \sqrt{16 \cdot 4 \cdot 121} = \sqrt{7744}= 88 \: см^2

Ответ: 88 см²

Проверка .

Задача 7

Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.

Решение

Для решения этой задачи воспользуемся формулой.

S = \dfrac{1}{2}(b^2-a^2) \cdot \tg(\alpha) = \dfrac{1}{2}(8^2-6^2) \cdot \tg(45°)

Тангенс 45° = 1, продолжим вычисления:

S = \dfrac{1}{2}(8^2-6^2) \cdot \tg(45°) = \dfrac{1}{2}(64-36) \cdot 1 = \dfrac{1}{2} \cdot 28 = 14 \: см^2

Ответ: 14 см²

Убедиться в правильности решения нам поможет калькулятор .

Применение в реальной жизни

Знание того, как вычислить площадь трапеции, может пригодиться не только на уроках геометрии. Вот несколько примеров:

  • Расчет площади участка земли неправильной формы
  • Вычисление площади крыши дома
  • Определение количества материала для пошива трапециевидной юбки

❓ Ответы на вопросы

Что такое трапеция?

Трапеция - это четырехугольник с двумя параллельными сторонами разной длины, которые называются основаниями.

Как вычислить площадь трапеции?

Площадь трапеции вычисляется по формуле: S = (a + b) * h / 2, где a и b - длины оснований, а h - высота трапеции.

Что такое высота трапеции?

Высота трапеции - это перпендикуляр, проведенный от одного основания к другому (или его продолжению).

Может ли трапеция иметь равные основания?

Да, может. В этом случае трапеция становится прямоугольником, который является частным случаем трапеции.

Как найти площадь равнобедренной трапеции?

Площадь равнобедренной трапеции находится по той же формуле, что и для обычной трапеции: S = (a + b) * h / 2.

Что делать, если известны только боковые стороны и основания трапеции?

В этом случае сначала нужно найти высоту трапеции, используя теорему Пифагора, а затем применить стандартную формулу площади.

Существуют ли другие способы нахождения площади трапеции?

Да, есть альтернативные методы: через среднюю линию, с помощью диагоналей и угла между ними, а также метод разбиения на простые фигуры.

Как связаны площади трапеции и треугольника?

Если разделить трапецию по диагонали, получатся два треугольника. Сумма их площадей равна площади трапеции.

Влияет ли наклон боковых сторон на площадь трапеции?

Наклон боковых сторон не влияет на площадь напрямую. Важны только длины оснований и высота трапеции.

Можно ли найти площадь трапеции, если известен только ее периметр?

Нет, одного периметра недостаточно. Нужны дополнительные данные, как минимум длины оснований и высота.

Надеюсь, теперь тема площади трапеции стала для вас немного яснее. Главное - не бояться формул и понимать, откуда они берутся. Практикуйтесь, решайте задачи, и вскоре вы будете щелкать их как орешки!

А если останутся вопросы - не стесняйтесь спрашивать. Геометрия - это интересно, когда в ней разбираешься. Удачи в учебе!