На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Формула площади правильного многоугольника через длину стороны и число сторон
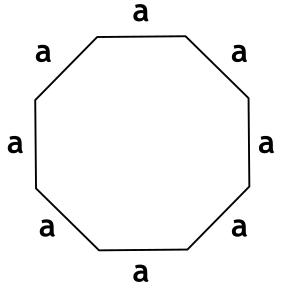
S = \dfrac{na^2}{4} \cdot \ctg \dfrac{180°}{n}
a - длина стороны многоугольника
n - число сторон многоугольника
Формула площади правильного многоугольника через радиус вписанной окружности
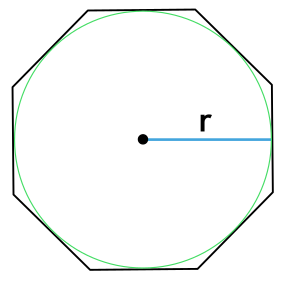
S = nr^2 \tg \dfrac{180°}{n}
r - радиус вписанной в многоугольник окружности
n - число сторон многоугольника
Формула площади правильного многоугольника через радиус описанной окружности

S = \dfrac{nR^2}{2} \cdot \sin \dfrac{360°}{n}
R - радиус описанной в многоугольник окружности
n - число сторон многоугольника
Пример задачи на нахождение площади правильного многоугольника
Задача 1
Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r - радиус вписанной окружности.
Решение
Чтобы решить эту задачу мы используем вторую формулу.
S = nr^2 \tg \dfrac{180°}{n} = 6 \cdot 9^2 \cdot \tg \dfrac{180°}{6} = 6 \cdot 81 \cdot \tg 30° = 486 \cdot \tg 30° = 486 \cdot 0.57735027 \approx 280.59223 \: см^2Ответ: 486 \cdot \tg 30° \approx 280.59223 \: см^2
Чтобы проверить ответ воспользуемся калькулятором .