Площадь кольца через радиусы
{S = \pi (R^2 - r^2)}
Найти площадь кольца
Внешний радиус R
Внутренний радиус r
Результат в
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать

С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.

Содержание:
  1. калькулятор площади кольца
  2. формула площади кольца через радиусы
  3. формула площади кольца через диаметры
  4. примеры задач

Формула площади кольца через радиусы

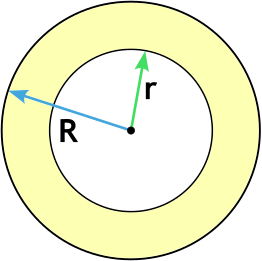
Площадь кольца через радиусы
{S = \pi (R^2 - r^2)}

R - внешний радиус кольца

r - внутренний радиус кольца

Формула площади кольца через диаметры

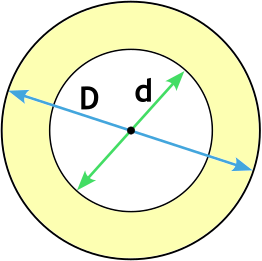
Площадь кольца через диаметры
{S= \dfrac{\pi}{4}(D^2 - d^2)}

D - внешний диаметр кольца

d - внутренний диаметр кольца

Примеры задач на нахождение площади кольца

Задача 1

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.

Решение

В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.

S = \pi (R^2 - r^2) = \pi (7^2 - 3^2) = \pi (49 - 9) = 40\pi \approx 125.66371 \: см^2

Ответ: 108 \cdot 0.866 \approx 93.53074 \: см^2

Полученный ответ можно проверить с помощью калькулятора .

Задача 2

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны \dfrac{4}{\sqrt{\pi}} и \dfrac{2}{\sqrt{\pi}}.

Решение

Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.

S = \pi (R^2 - r^2) = \pi ({\Big(\dfrac{4}{\sqrt{\pi}} \Big) }^2 - {\Big(\dfrac{2}{\sqrt{\pi}} \Big) }^2) = \pi (\dfrac{16}{\pi} - \dfrac{4}{\pi}) = \pi \dfrac{12}{\pi} = 12 \: см^2

Ответ: 12 \: см^2

Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:

\dfrac{4}{\sqrt{\pi}} \: \rarr \: 4/sqrt(pi)

\dfrac{2}{\sqrt{\pi}} \: \rarr \: 2/sqrt(pi)

Если ввести данные в таком формате, можно проверить ответ .

Задача 3

Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.

Решение

Задача аналогична предыдущим.

S = \pi (R^2 - r^2) = \pi (15^2 - 13^2) = \pi (225 - 169) = 56\pi \approx 175.92919 \: см^2

Ответ: 56\pi \approx 175.92919 \: см^2

Проверка .

Задача 4

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

Решение

Задача аналогична предыдущим.

S = \pi (R^2 - r^2) = \pi (13^2 - 12^2) = \pi (169 - 144) = 25\pi \approx 78.53982 \: см^2

Ответ: 25\pi \approx 78.53982 \: см^2

Проверка .