На этой странице с помощью калькулятора и формулы можно найти площадь сектора кольца через радиусы и угол сектора кольца.
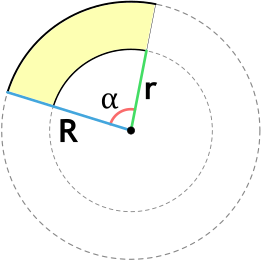
Сектор кольца — это часть круга, ограниченная дугами разных радиусов, проведенных из одной точки - центра, и двумя радиусами, проведенными к концам дуги большего радиуса..
Формула площади сектора кольца для угла в градусах
{S = \pi \dfrac{\alpha °}{360°}(R^2 - r^2)}
R - внешний радиус кольца
r - внутренний радиус кольца
α - угол сектора кольца (в градусах)
Формула площади сектора кольца для угла в радианах

{S = \dfrac{\alpha}{2}(R^2 - r^2)}
R - внешний радиус кольца
r - внутренний радиус кольца
α - угол сектора кольца (в радианах)
Пример задачи на нахождение площади сектора кольца
Задача 1
Найдите площадь сектора кольца, если внешний радиус кольца 5 см, внутренний радиус 3см, а угол сектора 45 градусов.
Решение
Подставим значения из условия в первую формулу и произведем расчет.
S = \pi \dfrac{\alpha °}{360°}(R^2 - r^2) = \pi \dfrac{45 °}{360°}(5^2 - 3^2) = \pi \dfrac{1}{8}(25 - 9) = \pi \dfrac{1}{8} \cdot 16 = 2\pi \: см^2 \approx 6.28319 \: см^2Ответ: 2\pi \: см^2 \approx 6.28319 \: см^2
Проверить правильность решения задачи нам поможет калькулятор .