На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Формула объема пирамиды
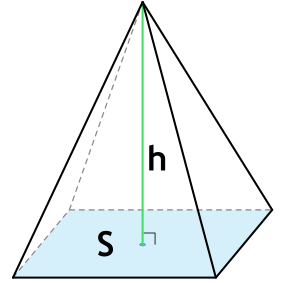
S - площадь основания пирамиды
h - высота пирамиды
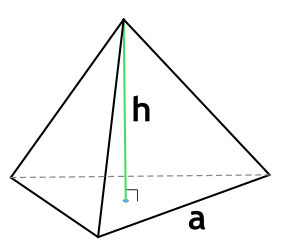
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида - пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
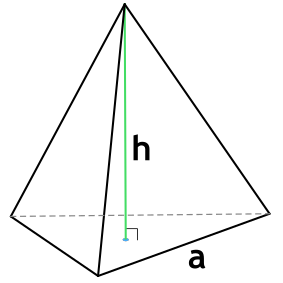
a - длина стороны основания пирамиды
h - высота пирамиды
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида - пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
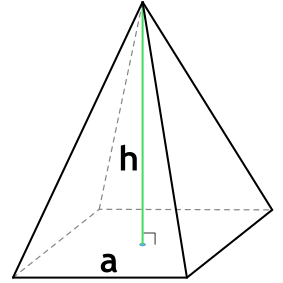
a - длина стороны основания пирамиды
h - высота пирамиды
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида - пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
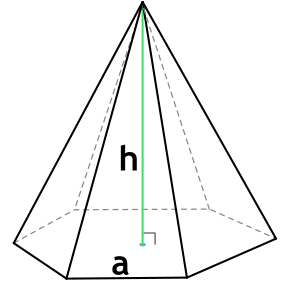
a - длина стороны основания пирамиды
h - высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

a - длина стороны основания пирамиды
h - высота пирамиды
n - число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр - правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
a - длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= \dfrac{1}{3} \cdot h \cdot a^2 = \dfrac{1}{3} \cdot 2 \cdot 3^2 = \dfrac{1}{3} \cdot 2 \cdot 9 = \dfrac{1}{3} \cdot 18 = 6 \: м^3Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= \dfrac{h \cdot a^2}{4 \sqrt{3}} = \dfrac{\sqrt{3} \cdot 1^2}{4 \sqrt{3}} = \dfrac{\sqrt{3} \cdot 1}{4 \sqrt{3}} = \dfrac{\sqrt{3}}{4 \sqrt{3}} = \dfrac{\cancel{\sqrt{3}}}{4 \cancel{\sqrt{3}}} = \dfrac{1}{4} = 0.25 \: м^3Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.