На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды - это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды - это совокупная площадь всех боковых граней пирамиды.
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему

P - периметр основания пирамиды
L - апофема пирамиды
S - площадь основания пирамиды
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
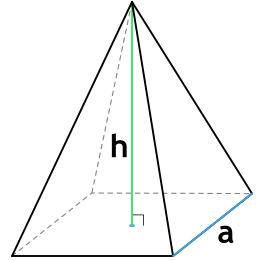
a - сторона основания пирамиды
h - высота пирамиды
n - число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
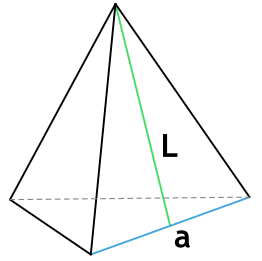
a - сторона основания пирамиды
L - апофема пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
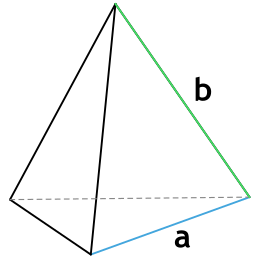
a - сторона основания пирамиды
b - боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
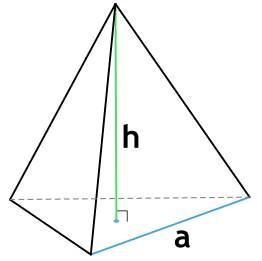
a - сторона основания пирамиды
h - высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
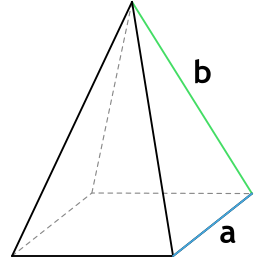
a - сторона основания пирамиды
b - боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту

a - сторона основания пирамиды
h - высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему

a - сторона основания пирамиды
L - апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему

a - сторона основания пирамиды
L - апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
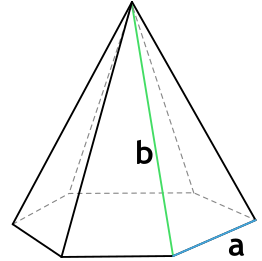
a - сторона основания пирамиды
b - боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту

a - сторона основания пирамиды
h - высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
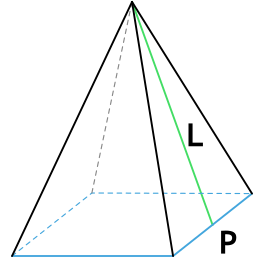
P - периметр основания пирамиды
L - апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту

a - сторона основания пирамиды
h - высота пирамиды
n - число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
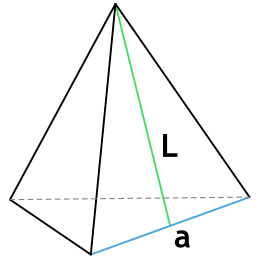
a - сторона основания пирамиды
L - апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
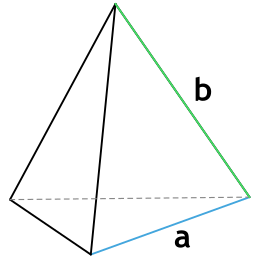
a - сторона основания пирамиды
b - боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
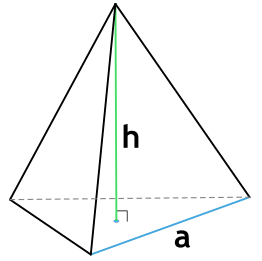
a - сторона основания пирамиды
h - высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
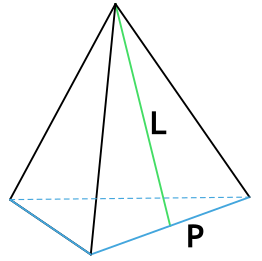
P - периметр основания пирамиды
L - апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
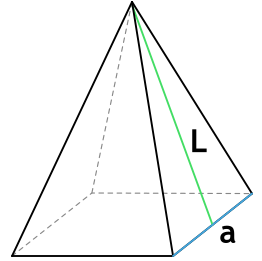
a - сторона основания пирамиды
L - апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
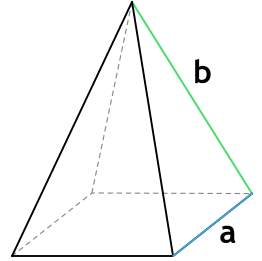
a - сторона основания пирамиды
b - боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
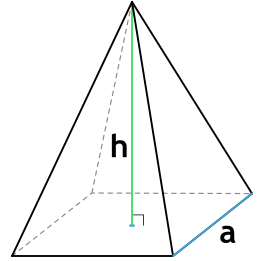
a - сторона основания пирамиды
h - высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему

a - сторона основания пирамиды
L - апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань

a - сторона основания пирамиды
b - боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту

a - сторона основания пирамиды
h - высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a \sqrt{b^2- \dfrac{a^2}{4}} = 60^2 + 2 \cdot 60 \sqrt{78^2- \dfrac{60^2}{4}} = 3600 + 120 \sqrt{6084- \dfrac{3600}{4}} = 3600 + 120 \sqrt{6084 - 900} = 3600 + 120 \sqrt{5184} = 3600 + 120 \cdot 72 = 3600 + 8640 = 12240 \: см²Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = \dfrac{3}{2}aL = \dfrac{3}{2} \cdot 6 \cdot 10 = \dfrac{3}{2} \cdot 60 = 90 \: см²Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a \sqrt{h^2+ \Bigg( \dfrac{a}{2 \tg ( 45°)} \Bigg) ^2} = 2 \cdot 6 \sqrt{4^2+ \Bigg( \dfrac{6}{2 \tg ( 45°)} \Bigg) ^2} = 60 \: см²Ответ: 60 см²
Проверка .