Куб - это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Формула объёма куба через ребро
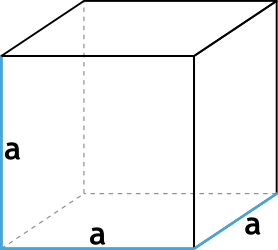
{V=a ^ 3}
a - ребро куба
Формула объёма куба через диагональ грани
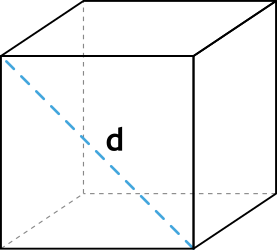
{V = \Big( \dfrac{d}{\sqrt{2}} \Big) ^3}
d - диагональ грани куба
Формула объёма куба через периметр грани
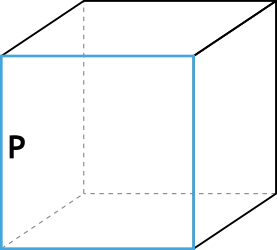
{V= \Big( \dfrac{P}{4} \Big) ^3}
P - периметр грани куба
Формула объёма куба через диагональ куба
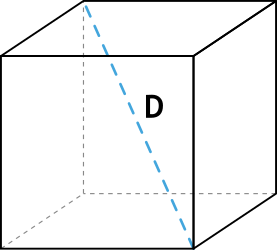
{V= \dfrac{D^3}{3\sqrt{3}}}
D - диагональ куба
Формула объёма куба через площадь полной поверхности
{V= \dfrac{\sqrt{{S_{полн}}^3}}{6\sqrt{6}}}
Sполн - диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 \: см^3Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= \dfrac{\sqrt{{S_{полн}}^3}}{6\sqrt{6}} = \dfrac{\sqrt{{96}^3}}{6\sqrt{6}} = \dfrac{\sqrt{96 \cdot 96 \cdot 96}}{6\sqrt{6}} = \dfrac{96 \sqrt{96}}{6\sqrt{6}} = \dfrac{96 \sqrt{16 \cdot 6}}{6\sqrt{6}} = \dfrac{96 \cdot 4 \sqrt{6}}{6\sqrt{6}} = \dfrac{384 \sqrt{6}}{6\sqrt{6}} = 64 \: см^3Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.