Объем параллелепипеда
{V= a \cdot b \cdot c}
Найти объем
Найти объем через
Сторона a
Сторона b
Сторона c
Результат в
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать

Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.

Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Содержание:
  1. калькулятор объема параллелепипеда
  2. формула объема прямоугольного параллелепипеда через три стороны
  3. формула объема прямоугольного параллелепипеда через площадь основания и высоту
  4. формула объема наклонного параллелепипеда через длины сторон основания и высоту
  5. формула объема наклонного параллелепипеда через площадь основания и высоту
  6. примеры задач

Формула объема прямоугольного параллелепипеда через три стороны

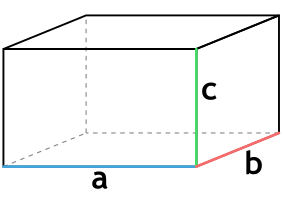
Объем прямоугольного параллелепипеда через три стороны
{V= a \cdot b \cdot c}

a - длина параллелепипеда

b - ширина параллелепипеда

c - высота параллелепипеда

Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab - это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}

Формула объема прямоугольного параллелепипеда через площадь основания и высоту

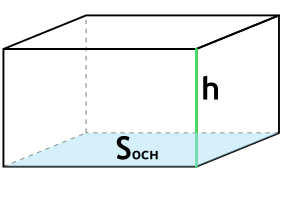
Объем прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} \cdot h}

Sосн - площадь основания параллелепипеда

h - высота параллелепипеда

Формула объема наклонного параллелепипеда через длины сторон основания и высоту

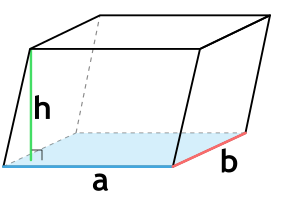
Объем наклонного параллелепипеда через длины сторон основания и высоту
{V= a \cdot b \cdot h}

a - длина основания параллелепипеда

b - ширина основания параллелепипеда

h - высота параллелепипеда

Формула объема наклонного параллелепипеда через площадь основания и высоту

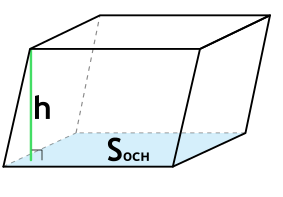
Объем наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} \cdot h}

Sосн - площадь основания параллелепипеда

h - высота параллелепипеда

Примеры задач на нахождение объема параллелепипеда

Задача 1

Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.

Решение

Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.

V= a \cdot b \cdot c = 3 \cdot 4 \cdot 5 = 60 \: см^3

Ответ: 60 см³

Проверим правильность ответа с помощью калькулятора .

Задача 2

Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.

Решение

Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.

V= S_{осн} \cdot h = 12 \cdot 3 = 36 \: м^3

Ответ: 36 м³

Полученный ответ поможет проверить калькулятор .