Конус - это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра - высоту (h) и радиус основания (r).
Если мы сравним формулу объема конуса с формулой объема цилиндра, то мы увидим, что объем конуса в 3 раза меньше объема цилиндра с той же высотой и радиусом основания.
Наш калькулятор может рассчитать объем конуса через радиус основания и высоту, площадь основания и высоту, а также объем усеченного конуса через его высоту и радиусы нижнего и верхнего оснований.
Кроме того объем конуса можено найти, подставив значения в формулы, приведенные ниже.
Формула объёма конуса через радиус и высоту
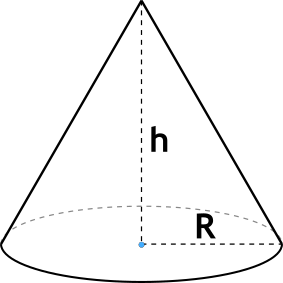
r - радиус основания конуса,
h - высота конуса
Формула объёма конуса через площадь основания и высоту
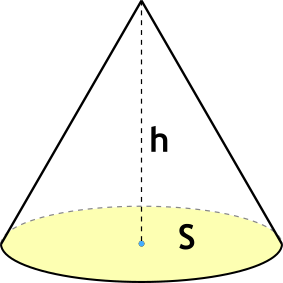
S - площадь основания конуса,
h - высота конуса
Формула объёма усеченного конуса
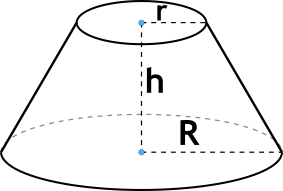
h - высота усеченного конуса,
r - радиус меньшего основания усеченного конуса,
R - радиус большего основания усеченного конуса.
Примеры задач на нахождение объема конуса
Задача 1
Решение
Подставим эти значения в формулу и произведем расчет:
V=\dfrac {1}{3} \pi r^2 h = \dfrac {1}{3} \cdot \pi \cdot 20^2 \cdot 30 = \dfrac {1}{3} \cdot \pi \cdot 12000 = 400 \pi \: см^3 \approx 12 566,37 \: см^3Ответ: {400 \pi \: см^3 \approx 12 566,37 \: см^3}
Проверить результат можно с помощью калькулятора .
Задача 2
Решение
Подставим эти значения в формулу и произведем расчет:
V=\dfrac {1}{3} S h = \dfrac {1}{3} \cdot 8 \cdot 3 = \dfrac {1}{3} \cdot 24 = 8 \: см^3Ответ: 8 см³
Воспользуемся калькулятором для проверки результата.
Задача 3
Решение
Подставим высоту и радиусы оснований в формулу и произведем расчет:
V=\dfrac {1}{3} \pi h(r^2 + r R + R^2) = \dfrac {1}{3} \pi \cdot 3 \cdot (1^2 + 1 \cdot 2 + 2^2) = \dfrac {1}{3} \pi \cdot 3 \cdot (1 + 2 + 4) = \dfrac {1}{3} \pi \cdot 3 \cdot 7 = \dfrac {1}{3} \pi \cdot 21 = 7 \pi \: см^3 \approx 21,99115 \: см^3Ответ: {7 \pi \: см^3 \approx 21,99115 \: см^3}
Проверим полученный ответ.