Объем шарового сегмента
{V = \pi h^2 \Big( R - \dfrac{1}{3} h \Big) }
Радиус R
Высота сегмента h
Результат в
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать

На странице содержится калькулятор и формула для расчета объема шарового сегмента. Введите радиус шара и высоту сегмента и тут же получите результат.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.

Содержание:
  1. калькулятор объема шарового сегмента
  2. формула объема шарового сегмента
  3. примеры задач

Формула объёма шарового сегмента

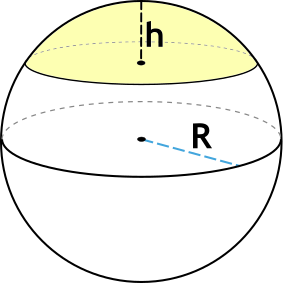
Объем куба через ребро
{V = \pi h^2 \Big( R - \dfrac{1}{3} h \Big)}

R - радиус шара

h - высота шарового сегмента

Примеры задач на нахождение объема шарового сегмента

Задача 1

Найдите обьем шарового сектора,если радиус шара равен 6см,а высота соответствующего сегмента составляет шестую часть диаметра шара.

Решение

Для решения задачи нам сначала необходимо найти высоту шарового сегмента. Помня о том, что диаметр - это два радиуса, получим, что диаметр шара составляет 2 • 6см = 12см. А так как высота шарового сегмента составляет шестую часть диаметра, то поделим 12см на 6 и получим высоту шарового сегмента 2см.

Теперь осталось применить формулу, подставив в нее значения и произвести вычисления.

V = \pi h^2 \Big( R - \dfrac{1}{3} h \Big) = \pi \cdot 2^2 \cdot \Big( 6 - \dfrac{1}{3} 2 \Big) = \pi \cdot 4 \cdot \dfrac{16}{3} = \dfrac{64}{3} \pi \: см^3

Получившаяся дробь является неправильной, ее можно преобразовать в смешанную.

\dfrac{64}{3} = 21\dfrac{1}{3}

Итоговый ответ можно записать так 21\dfrac{1}{3} \pi \: см^3 \approx 67.02064 \: см^3

Ответ: 21\dfrac{1}{3} \pi \: см^3 \approx 67.02064 \: см^3

Осталось проверить ответ с помощью калькулятора .