Здесь вы можете рассчитать площадь сектора круга с помощью удобного онлайн калькулятора по двум формулам. Для этого необходимо ввести известные вам параметры фигуры:
- радиус круга и угол,
- длину дуги и радиус.
Сектор круга или окружности - это его(её) часть, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (окружности).
Формула площади сектора круга через радиус и угол
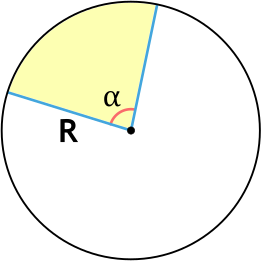
R - радиус сектора
α° - угол сектора (в градусах)
α - угол сектора (в радианах)
Формула площади сектора круга через радиус и длину дуги

L - длина дуги сектора
R - радиус сектора
Примеры задач на нахождение площади сектора круга
Задача 1
Решение
Для решения задачи нам подойдет вторая формула.
S = \dfrac{1}{2}LR = \dfrac{1}{2} \cdot 2 \cdot 1 = \dfrac{1}{2} \cdot 2 = 1 \: см^2Ответ: 1 \: см^2
Давайте проверим ответ с помощью калькулятора .
Задача 2
Решение
Задача аналогична предыдущей.
S = \dfrac{1}{2}LR = \dfrac{1}{2} \cdot 3 \cdot 24 = \dfrac{1}{2} \cdot 72 = 36 \: см^2Ответ: 36 \: см^2
Проверка .
Задача 3
Решение
Для решения этой задачи нам потребуется первая формула, в которой угол указывается в градусах.
S = \pi R^2 \dfrac{\alpha °}{360°} = \pi \cdot 3^2 \cdot \dfrac{120°}{360°} = \pi \cdot 9 \cdot \dfrac{1}{3} = 3 \pi \: см^2 \approx 9.42478 \: см^2Ответ: 3 \pi \: см^2 \approx 9.42478 \: см^2
Проверка .