На странице содержится информация о теореме синусов, калькулятор, с помощью которого можно найти стороны и угол треугольника, а также формула теоремы синусов.
Теорема синусов — теорема, которая устанавливает зависимость между сторонами треугольника и величиной противолежащих им углов.
Стороны треугольника пропорциональны синусам противолежащих углов.
Кроме того теорему синусов можно записать в расширенной форме. В этом случае в нее добавляется значение радиуса описанной окружности треугольника.
Формула теоремы синусов
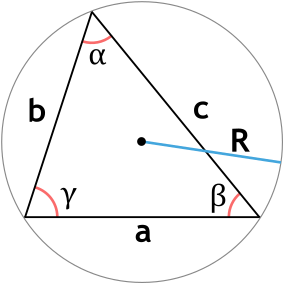
{\dfrac{a}{\sin \alpha} = \dfrac{b}{\sin \beta} = \dfrac{c}{\sin \gamma} = 2R}
a, b, c - стороны треугольника,
α, β, γ - углы треугольника.
R - радиус описанной около треугольника окружности.