Страница содержит полную информацию о теореме косинусов, а также калькулятор, с помощью которого можно найти стороны и угол треугольника и формулу теоремы косинусов.
Теорема косинусов обобщает теорему Пифагора на произвольные плоские треугольники и устанавливает соотношение между сторонами треугольника и его углами.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов
{a^2 = b^2 + c^2-2bc \cos (\alpha)}
{b^2 = a^2 + c^2-2ac \cos (\beta)}
{c^2 = a^2 + b^2-2ab \cos (\gamma)}
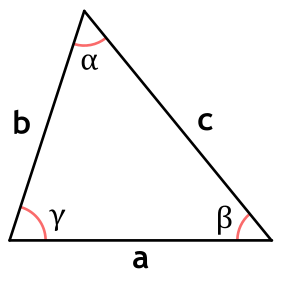
a, b, c - стороны треугольника,
α, β, γ - углы треугольника.