Чтобы найти периметр треугольника необходимо сложить длины трех его сторон. Однако, существует множество других формул, которые позволяют рассчитать периметр треугольника. На странице мы собрали самые известные формулы для расчета периметра треугольника, а также удобный калькулятор.
Содержание:
- калькулятор периметра треугольника
- формула периметра треугольника через стороны
- формула периметра треугольника по средним линиям
- формула периметра треугольника по двум сторонам и углу между ними
- формула периметра прямоугольного треугольника по катету и гипотенузе
- формула периметра прямоугольного треугольника по катетам
- формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
- формула периметра прямоугольного треугольника по катету и прилежащему углу
- формула периметра прямоугольного треугольника по катету и противолежащему углу
- формула периметра равнобедренного треугольника по боковой стороне и высоте
- формула периметра равнобедренного треугольника по основанию и высоте
- формула периметра равнобедренного треугольника по боковой стороне и основанию
- формула периметра равностороннего треугольника по высоте
- формула периметра равностороннего треугольника через площадь вписанной окружности
- примеры задач
Треугольник - геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки.
Формула периметра треугольника через стороны

a, b и c - стороны треугольника
Формула периметра треугольника по средним линиям
Средняя линия треугольника — отрезок, который соединяет середины двух сторон.

a, b и c - средние линии треугольника
Формула периметра треугольника по двум сторонам и углу между ними
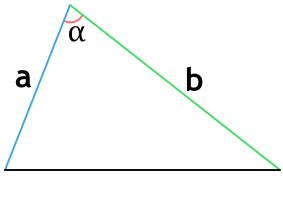
a и b - стороны треугольника
α - угол между сторонами a и b
Формула периметра прямоугольного треугольника по катету и гипотенузе
Прямоугольный треугольник — это треугольник, в котором один угол прямой (90 градусов).

a - катет прямоугольного треугольника
c - гипотенуза прямоугольного треугольника
Формула периметра прямоугольного треугольника по катетам

a и b - катеты прямоугольного треугольника
Формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу

c - гипотенуза прямоугольного треугольника
α - прилежащий к гипотенузе угол
Формула периметра прямоугольного треугольника по катету и прилежащему углу

a - катет прямоугольного треугольника
α - прилежащий к катеру угол
Формула периметра прямоугольного треугольника по катету и противолежащему углу

a - катет прямоугольного треугольника
α - противолежащий к катеру угол
Формула периметра равнобедренного треугольника по боковой стороне и высоте
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
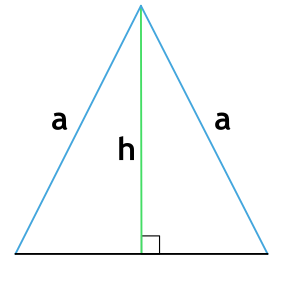
a - боковая сторона равнобедренного треугольника
h - высота равнобедренного треугольника
Формула периметра равнобедренного треугольника по основанию и высоте
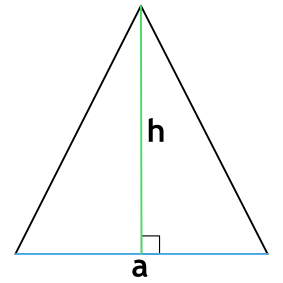
a - основание равнобедренного треугольника
h - высота равнобедренного треугольника
Формула периметра равнобедренного треугольника по боковой стороне и основанию

a - основание равнобедренного треугольника
b - боковая сторона равнобедренного треугольника
Формула периметра равностороннего треугольника по высоте
Равносторонний треугольник —треугольник, у которого все стороны равны.
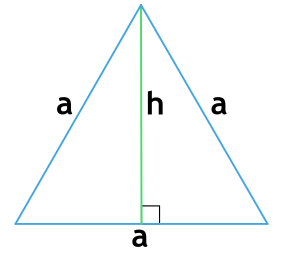
h - высота равностороннего треугольника
Формула периметра равностороннего треугольника через площадь вписанной окружности

S - площадь вписанной в равносторонний треугольник окружности
Примеры задач на нахождение периметра треугольника
Задача 1
Решение
Для решения задачи применим формулу №2. Подставим в нее длины средних линий и произведем вычисления.
P = 2a+2b+2c = 2 \cdot 6 + 2 \cdot 9 + 2 \cdot 10 = 12 + 18 + 20 = 50 \: смОтвет: 50 см
Ответ проверим с помощью калькулятора .
Задача 2
Решение
А для этой задачи подойдет первая формула.
P = a+b+c = 14 + 17 + 17 = 48 \: смЕсли обратить внимание на то, что у треугольника в условии две стороны имеют одинаковую длину, то можно понять, что данный треугольник равнобедренный. И тогда задачу можно решить используя формулу для равнобедренного треугольника.
P=2b+a = 2 \cdot 17 + 14 = 34 + 14 = 48 \: смОтвет: 48 см
Задача 3
Решение
Воспользуемся подходящей формулой.
P = a+b+\sqrt{a^2+b^2} = 12+16+\sqrt{12^2+16^2} = 28+\sqrt{144+256} = 28+\sqrt{400} = 28+20 = 48 \: смОтвет: 48 см
Полученный результат удобно проверить с помощью калькулятора .
Задача 4
Решение
Для равнобедренного треугольника, у которого известно основание и боковая сторона нам подходит эта формула.
P=2b+a = 2 \cdot 8 + 13 = 16 + 13 = 29 \: смОтвет: 29 см
Проверка .
Задача 5
Решение
Для равностороннего треугольника с известной высотой мы применим эту формулу.
P = 2\sqrt{3}h = 2\sqrt{3} \cdot 9 = 18\sqrt{3} \: см \approx 31.17691 \: смОтвет: 18\sqrt{3} \: см \approx 31.17691 \: см
Проверить ответ поможет калькулятор .