На этой странице находится все необходимое, чтобы найти расстояние между двумя точками. Просто введите координаты точек и получите ответ и подробное решение с помощью наших онлайн-калькуляторов. Кроме того на сайте можно найти координаты середины отрезка.
Расстояние между двумя точками - это длина отрезка, соединяющего эти точки.
Формула расстояния между двумя точками на плоскости:
xa и ya - координаты первой точки A,
xb и yb - координаты второй точки B
Нахождение расстояния между двумя точками на плоскости сводится к решению треугольника, а точнее - нахождению его гипотенузы. Для этого используется теорема Пифагора. Посмотрите на рисунок.
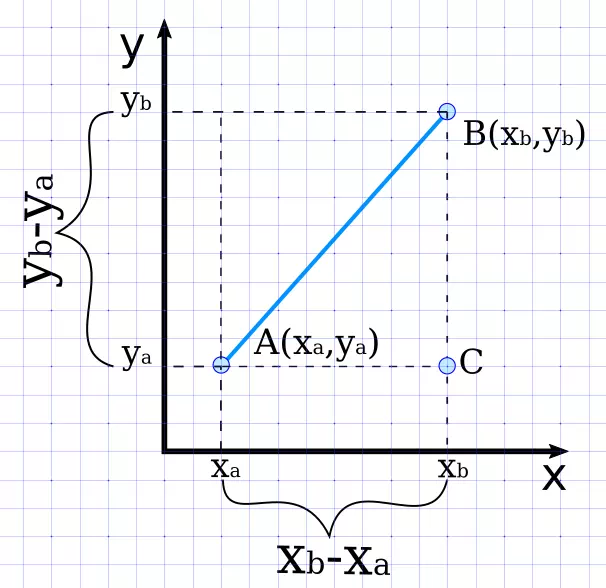
Соединив отрезком точки A и B, а также опустив перпендикуляры на оси мы получим треугольник ABC. В этом треугольнике стороны AC и BC являются катетами прямоугольного треугольника, а AB - его гипотенузой. Длины катетов AC и BC найти довольно просто:
AC = xb - xa
BC = yb - ya
Осталось применить теорему Пифагора и получить сторону AB, которая является гипотенузой прямоугольного треугольника и расстоянием между точками A и B:
AB=\sqrt{{AC}^2 + {BC^2}}
Подставив вместо отрезков AC и BC их длины, получим итоговую формулу расстояния между двумя точками:
AB=\sqrt{{(x_b - x_a)}^2 + {(y_b - y_a)^2}} или d=\sqrt{{(x_b - x_a)}^2 + {(y_b - y_a)^2}}
Формула расстояния между двумя точками в пространстве:
xa, ya и za - координаты первой точки A,
xb, yb и zb - координаты второй точки B
Примеры задач на вычисление середины отрезка
Задача 1
Решение
Подставим координаты точек в формулу расстояния между двумя точками на плоскости и вычислим результат:
d=\sqrt{{(x_b - x_a)}^2 + {(y_b - y_a)^2}} = \sqrt{{(-2 - 2)}^2 + {(7 - 7)^2}} = \sqrt{{-4}^2 + {0^2}} = \sqrt{16 + 0} = \sqrt{16} = 4
Мы получили расстояние между точками и оно равно 4.
Ответ: 4.
Проверим результат с помощью калькулятора .