На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Содержание:
- калькулятор площади правильного шестиугольника
- формула площади правильного шестиугольника через длину стороны
- формула площади правильного шестиугольника через радиус вписанной окружности
- формула площади правильного шестиугольника через радиус описанной окружности
- формула площади правильного шестиугольника через периметр
- примеры задач
Формула площади правильного шестиугольника через длину стороны
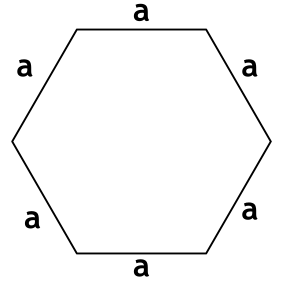
a - длина стороны шестиугольника
Формула площади правильного шестиугольника через радиус вписанной окружности
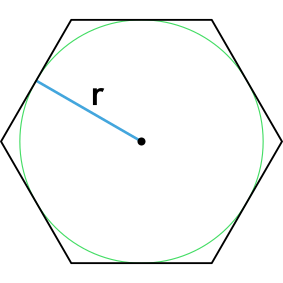
r - радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности

R - радиус описанной окружности
Формула площади правильного шестиугольника через периметр

P - периметр шестиугольника
Примеры задач на нахождение площади правильного шестиугольника
Задача 1
Решение
Исходя из того, что из условия задачи нам известен радиус вписанной окружности, мы воспользуемся формулой.
S = 2 \sqrt{3}r^2 = 2 \sqrt{3} \cdot 9^2 = 2 \sqrt{3} \cdot 81 = 162 \sqrt{3} \: см^2 \approx 280.59223 \: см^2Ответ: 162 \sqrt{3} \: см^2 \approx 280.59223 \: см^2
Проверить правильность решения нам поможет калькулятор .
Задача 2
Решение
Для этой задачи нам подойдет формула.
S = \dfrac{3 \sqrt{3} a^2}{2} = \dfrac{3 \sqrt{3} \cdot 1^2}{2} = \dfrac{3 \sqrt{3} \cdot 1}{2} = \dfrac{3 \sqrt{3}}{2} \: см^2 \approx 2.59808 \: см^2Ответ: \dfrac{3 \sqrt{3}}{2} \: см^2 \approx 2.59808 \: см^2